Portal:Mathematics - Wikipedia

The number π (; spelled out as "pi") is a mathematical constant that is the ratio of a circle's circumference to its diameter, approximately equal to 3.14159. The number π appears in many formulae across mathematics and physics. It is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found.

For thousands of years, mathematicians have attempted to extend their understanding of π, sometimes by computing its value to a high degree of accuracy. Ancient civilizations, including the Egyptians and Babylonians, required fairly accurate approximations of π for practical computations. Around 250 BC, the Greek mathematician Archimedes created an algorithm to approximate π with arbitrary accuracy. In the 5th century AD, Chinese mathematicians approximated π to seven digits, while Indian mathematicians made a five-digit approximation, both using geometrical techniques. The first computational formula for π, based on infinite series, was discovered a millennium later. The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by the Welsh mathematician William Jones in 1706. (Full article...)

Leonhard Euler ( OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] ^ⓘ,

Swiss Standard German: [ˈleːɔnhart ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician, and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory.

Euler is held to be one of the greatest, most prolific mathematicians in history and the greatest of the 18th century. Several great mathematicians who produced their work after Euler's death have recognised his importance in the field as shown by quotes attributed to many of them: Pierre-Simon Laplace expressed Euler's influence on mathematics by stating, "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss wrote: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." His 866 publications as well as his correspondences are being collected in the Opera Omnia Leonhard Euler which, when completed, will consist of 81 quartos. He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia. (Full article...)

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)

Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.

Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like (and) or (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design and manage programs that control risk. The actual steps needed to become an actuary are usually country-specific; however, almost all processes share a rigorous schooling or examination structure and take many years to complete. (Full article...)

Richard Phillips Feynman (; May 11, 1918 – February 15, 1988) was an American theoretical physicist, known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, as well as his work in particle physics for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.

Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)

In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.

The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).

In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)

In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as

The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
(Full article...)

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.

Every graph with n vertices has book thickness at most , and this formula gives the exact book thickness for complete graphs. The graphs with book thickness one are the outerplanar graphs. The graphs with book thickness at most two are the subhamiltonian graphs, which are always planar; more generally, every planar graph has book thickness at most four. All minor-closed graph families, and in particular the graphs with bounded treewidth or bounded genus, also have bounded book thickness. It is NP-hard to determine the exact book thickness of a given graph, with or without knowing a fixed vertex ordering along the spine of the book. Testing the existence of a three-page book embedding of a graph, given a fixed ordering of the vertices along the spine of the embedding, has unknown computational complexity: it is neither known to be solvable in polynomial time nor known to be NP-hard. (Full article...)

Sunday Osarumwense Iyahen (3 October 1937 – 28 January 2018) was a Nigerian mathematician and politician, recognised for his contributions to the field of topological vector spaces and his service as a senator representing Bendel Central Senatorial District. Born in Benin City, Edo State, Nigeria, Iyahen was the eldest of at least seventeen children and embarked on an academic journey that led him to earn a first-class honours degree in mathematics from the University of Ibadan and later a Ph.D. and D.Sc. from the University of Keele.

Iyahen's academic career was marked by his tenure as a professor of mathematics at several universities in Nigeria and abroad. He served as the Head of the Department of Mathematics and Dean of the Faculty of Science at the University of Ibadan before joining the Institute of Technology, Benin (now known as the University of Benin (Nigeria)), where he became the founding dean of the Faculty of Physical Sciences. His scholarly work includes over 100 published papers and contributions as editor-in-chief for mathematical journals. He was honoured with fellowships from the Nigerian Academy of Science and the Mathematical Association of Nigeria. As a politician, he was elected as a senator, where he contributed to national policy and development. (Full article...)

Arithmetic is an elementary branch of mathematics that studies numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.

Arithmetic systems can be distinguished based on the type of numbers they operate on. Integer arithmetic is about calculations with positive and negative integers. Rational number arithmetic involves operations on fractions of integers. Real number arithmetic is about calculations with real numbers, which include both rational and irrational numbers. (Full article...)

Aristotle (Greek: Ἀριστοτέλης Aristotélēs; 384–322 BC) was an Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, and the arts. As the founder of the Peripatetic school of philosophy in the Lyceum in Athens, he began the wider Aristotelian tradition that followed, which set the groundwork for the development of modern science.

Little is known about Aristotle's life. He was born in the city of Stagira in northern Greece during the Classical period. His father, Nicomachus, died when Aristotle was a child, and he was brought up by a guardian. At 17 or 18, he joined Plato's Academy in Athens and remained there until the age of 37 (c. 347 BC). Shortly after Plato died, Aristotle left Athens and, at the request of Philip II of Macedon, tutored his son Alexander the Great beginning in 343 BC. He established a library in the Lyceum, which helped him to produce many of his hundreds of books on papyrus scrolls. (Full article...)

In geometry and algebra, a real number is constructible if and only if, given a line segment of unit length, a line segment of length can be constructed with compass and straightedge in a finite number of steps. Equivalently, is constructible if and only if there is a closed-form expression for using only integers and the operations for addition, subtraction, multiplication, division, and square roots.

The geometric definition of constructible numbers motivates a corresponding definition of constructible points, which can again be described either geometrically or algebraically. A point is constructible if it can be produced as one of the points of a compass and straightedge construction (an endpoint of a line segment or crossing point of two lines or circles), starting from a given unit length segment. Alternatively and equivalently, taking the two endpoints of the given segment to be the points (0, 0) and (1, 0) of a Cartesian coordinate system, a point is constructible if and only if its Cartesian coordinates are both constructible numbers.^[1] Constructible numbers and points have also been called ruler and compass numbers and ruler and compass points, to distinguish them from numbers and points that may be constructed using other processes. (Full article...)

In the mathematical theory of minimal surfaces, the double bubble theorem states that the shape that encloses and separates two given volumes and has the minimum possible surface area is a standard double bubble: three spherical surfaces meeting at angles of 120° on a common circle. The double bubble theorem was formulated and thought to be true in the 19th century, and became a "serious focus of research" by 1989, but was not proven until 2002.

The proof combines multiple ingredients. Compactness of rectifiable currents (a generalized definition of surfaces) shows that a solution exists. A symmetry argument proves that the solution must be a surface of revolution, and it can be further restricted to having a bounded number of smooth pieces. Jean Taylor's proof of Plateau's laws describes how these pieces must be shaped and connected to each other, and a final case analysis shows that, among surfaces of revolution connected in this way, only the standard double bubble has locally-minimal area. (Full article...)

A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.

Several methods are known for defining cellular automata rules that are reversible; these include the block cellular automaton method, in which each update partitions the cells into blocks and applies an invertible function separately to each block, and the second-order cellular automaton method, in which the update rule combines states from two previous steps of the automaton. When an automaton is not defined by one of these methods, but is instead given as a rule table, the problem of testing whether it is reversible is solvable for block cellular automata and for one-dimensional cellular automata, but is undecidable for other types of cellular automata. (Full article...)

Bernt Michael Holmboe (23 March 1795 – 28 March 1850) was a Norwegian mathematician. He was home-tutored from an early age, and was not enrolled in school until 1810. Following a short period at the Royal Frederick University, which included a stint as assistant to Christopher Hansteen, Holmboe was hired as a mathematics teacher at the Christiania Cathedral School in 1818, where he met the future renowned mathematician Niels Henrik Abel. Holmboe's lasting impact on mathematics worldwide has been said to be his tutoring of Abel, both in school and privately. The two became friends and remained so until Abel's early death. Holmboe moved to the Royal Frederick University in 1826, where he worked until his own death in 1850.

Holmboe's significant impact on mathematics in the fledgling Norway was his textbook in two volumes for secondary schools. It was widely used, but faced competition from Christopher Hansteen's alternative offering, sparking what may have been Norway's first debate about school textbooks. (Full article...)

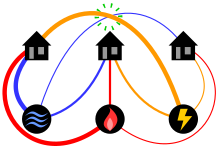
The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.

This puzzle can be formalized as a problem in topological graph theory by asking whether the complete bipartite graph , with vertices representing the houses and utilities and edges representing their connections, has a graph embedding in the plane. The impossibility of the puzzle corresponds to the fact that is not a planar graph. Multiple proofs of this impossibility are known, and form part of the proof of Kuratowski's theorem characterizing planar graphs by two forbidden subgraphs, one of which is . The question of minimizing the number of crossings in drawings of complete bipartite graphs is known as Turán's brick factory problem, and for the minimum number of crossings is one. (Full article...)

Fast inverse square root, sometimes referred to as Fast InvSqrt() or by the hexadecimal constant 0x5F3759DF, is an algorithm that estimates , the reciprocal (or multiplicative inverse) of the square root of a 32-bit floating-point number in IEEE 754 floating-point format. The algorithm is best known for its implementation in 1999 in Quake III Arena, a first-person shooter video game heavily based on 3D graphics. With subsequent hardware advancements, especially the x86 SSE instruction rsqrtss, this algorithm is not generally the best choice for modern computers, though it remains an interesting historical example.

The algorithm accepts a 32-bit floating-point number as the input and stores a halved value for later use. Then, treating the bits representing the floating-point number as a 32-bit integer, a logical shift right by one bit is performed and the result subtracted from the number

0x5F3759DF, which is a floating-point representation of an approximation of . This results in the first approximation of the inverse square root of the input. Treating the bits again as a floating-point number, it runs one iteration of Newton's method, yielding a more precise approximation. (Full article...)